Semester TWO:
Unit Four: Desmos Drawing Project and Function Families:
Reflection:
How did you go about drawing this image? (Did you plan? Did you use patterns, reflections of curves? Did you experiment? Did you consult with peers/teacher?) (3-5 sentences)
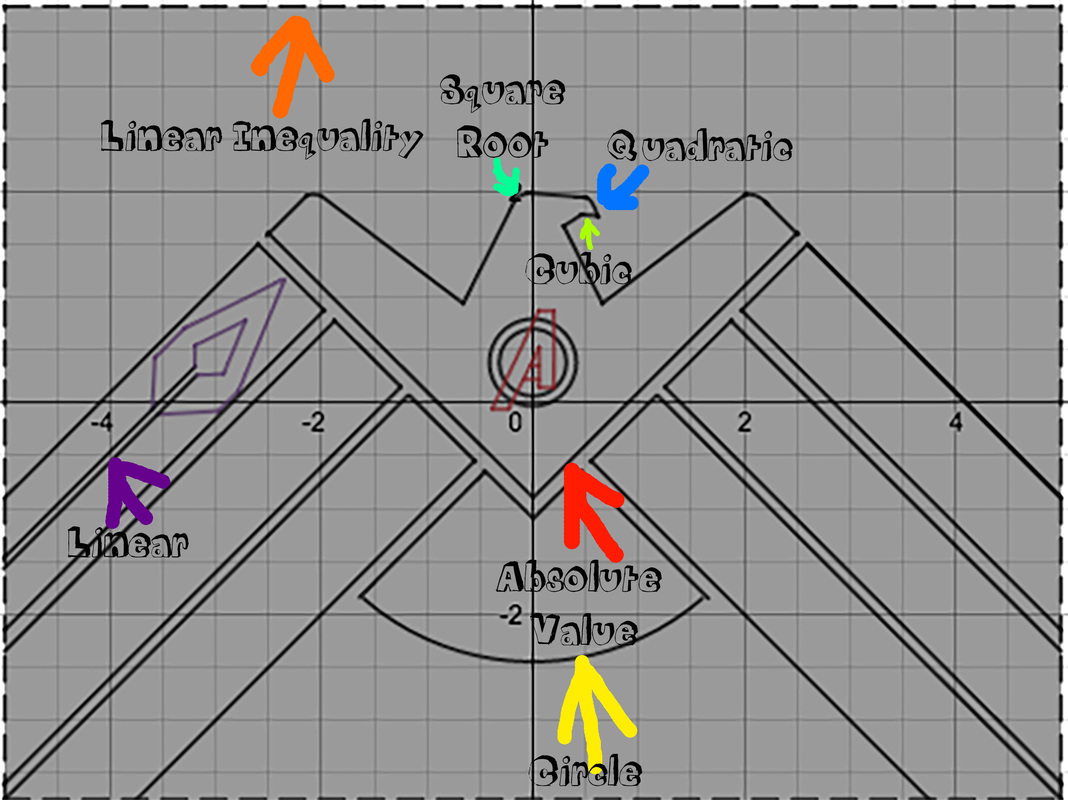
I decided on this image of the S.H.I.E.L.D. logo, because I really like the Avengers, and I thought it was a cool and challenging image to try to recreate. I experimented with many different types of functions such as, absolute value, square root, cubic, quadratic, and linear. I used the Function Family packet as a reference to see what the functions looked like and how to manipulate them. I experimented with slope, y-intercepts, h, and k to change the lines.
How did using Desmos and creating this drawing help you understand function families and their transformations? (Be specific and discuss two types of functions and what you learned about them - for example, discuss how you understand linear and quadratic functions.) (3-5 sentences)"
This project was really fun and helped me understand functions and their transformations. For example, I learned that when I was working with the eleven absolute value functions that I used in my drawing, restricting domain and range affects how much of the line shows. If you place restrictions on the range, both sides of the function show until the y restrictions. Restricting the domain and range affects other functions, such as quadratic, cubic, linear, and square root functions.
I decided on this image of the S.H.I.E.L.D. logo, because I really like the Avengers, and I thought it was a cool and challenging image to try to recreate. I experimented with many different types of functions such as, absolute value, square root, cubic, quadratic, and linear. I used the Function Family packet as a reference to see what the functions looked like and how to manipulate them. I experimented with slope, y-intercepts, h, and k to change the lines.
How did using Desmos and creating this drawing help you understand function families and their transformations? (Be specific and discuss two types of functions and what you learned about them - for example, discuss how you understand linear and quadratic functions.) (3-5 sentences)"
This project was really fun and helped me understand functions and their transformations. For example, I learned that when I was working with the eleven absolute value functions that I used in my drawing, restricting domain and range affects how much of the line shows. If you place restrictions on the range, both sides of the function show until the y restrictions. Restricting the domain and range affects other functions, such as quadratic, cubic, linear, and square root functions.
Unit three Reflection: Area, volume, measurement
Q1: What content/skills have been most interesting to you?
Volume, surface area, and calculator skills have been the most interesting concepts to me. The reason is because they are all relevant in the real world. They all have uses in different jobs. Using calculators also make you have to do less work, and make that work take less time.
Q2: How have you grown mathematically?
Throughout this unit I have not really grown mathematically. However, one new mathematical skill I did learn was how to use my calculator to complete repetitive math problems more efficiently. Most of the concepts that were taught in this unit I learned in middle school, such as area, surface area, and volume. However, some of the shapes were more complex to calculate for those values than I had previously learned. Although I did not learn many new concepts, old ones were strengthened.
Volume, surface area, and calculator skills have been the most interesting concepts to me. The reason is because they are all relevant in the real world. They all have uses in different jobs. Using calculators also make you have to do less work, and make that work take less time.
Q2: How have you grown mathematically?
Throughout this unit I have not really grown mathematically. However, one new mathematical skill I did learn was how to use my calculator to complete repetitive math problems more efficiently. Most of the concepts that were taught in this unit I learned in middle school, such as area, surface area, and volume. However, some of the shapes were more complex to calculate for those values than I had previously learned. Although I did not learn many new concepts, old ones were strengthened.
Unit Two Reflection:
Q1: What has been the work you are most proud of in this unit?
The work I am most proud of in this unit is the POW 3 – Solar POW. I worked harder on this POW than with others, because I felt connected to the topic. I saw the real world value of this POW. Most of the POWs didn’t appeal to me, but with this one I found it interesting because it touched on the topic of architecture/construction. Usually POWs are some of my worst grades, but this POW is my highest grade in geometry this semester. I think this result is because I enjoyed learning about the real world applications of trigonometry.
Q2: What skills are you developing in geometry/math? Skills can be applied across mathematics – think graphing, creating tables, creating diagrams or mathematical models, approaching problems in different ways (by testing cases, by testing extreme examples, by setting up a table initiating/approaching hard problems, e), or learning how to use your graphing calculator to fit equations to data.
I am developing several skills through geometry. One of the main skills that I am developing is creating mathematical models/diagrams. An example of this skill is shown in trigonometry problems. The first step in solving a trigonometry problem is drawing a diagram. For example, in the section of the course of geometry where we developed formulas by studying shadows, I created many diagrams. Also for POW 3 Solar POW I sketched a diagram to find the pitch of my roof. However, sometimes problems are worded in a different way, and I get confused with making the diagram, so there is still room for improvement in applying this strategy.
Q3: Choose one topic: similarity (ratios) or trigonometry. Explain what it is. Provide an example of how it is used in mathematics to solve problems. State an application of the topic in the adult world that interests you (i.e. scaled replicas of sculptures, gearing ratios, scaled models for architecture, trigonometry in construction or blood splatter analysis, etc).
Trigonometry is the study of the measures of triangles. An example of where trigonometry is used in math is when you are given a right triangle, and you only know the base and the lower left angle, and you have to figure out the area of the triangle. You could then take the tangent of the angle and make it equal the height divided by the base. You would then algebraically transform the equation to get the height on one side. An example of application of trigonometry in the real world could be architecture. You could be designing a building and know one side and an angle of triangular support you could then use a trigonometic ratio such as sine, cosine, or tangent to solve for the other angles and/or sides.
The work I am most proud of in this unit is the POW 3 – Solar POW. I worked harder on this POW than with others, because I felt connected to the topic. I saw the real world value of this POW. Most of the POWs didn’t appeal to me, but with this one I found it interesting because it touched on the topic of architecture/construction. Usually POWs are some of my worst grades, but this POW is my highest grade in geometry this semester. I think this result is because I enjoyed learning about the real world applications of trigonometry.
Q2: What skills are you developing in geometry/math? Skills can be applied across mathematics – think graphing, creating tables, creating diagrams or mathematical models, approaching problems in different ways (by testing cases, by testing extreme examples, by setting up a table initiating/approaching hard problems, e), or learning how to use your graphing calculator to fit equations to data.
I am developing several skills through geometry. One of the main skills that I am developing is creating mathematical models/diagrams. An example of this skill is shown in trigonometry problems. The first step in solving a trigonometry problem is drawing a diagram. For example, in the section of the course of geometry where we developed formulas by studying shadows, I created many diagrams. Also for POW 3 Solar POW I sketched a diagram to find the pitch of my roof. However, sometimes problems are worded in a different way, and I get confused with making the diagram, so there is still room for improvement in applying this strategy.
Q3: Choose one topic: similarity (ratios) or trigonometry. Explain what it is. Provide an example of how it is used in mathematics to solve problems. State an application of the topic in the adult world that interests you (i.e. scaled replicas of sculptures, gearing ratios, scaled models for architecture, trigonometry in construction or blood splatter analysis, etc).
Trigonometry is the study of the measures of triangles. An example of where trigonometry is used in math is when you are given a right triangle, and you only know the base and the lower left angle, and you have to figure out the area of the triangle. You could then take the tangent of the angle and make it equal the height divided by the base. You would then algebraically transform the equation to get the height on one side. An example of application of trigonometry in the real world could be architecture. You could be designing a building and know one side and an angle of triangular support you could then use a trigonometic ratio such as sine, cosine, or tangent to solve for the other angles and/or sides.
Semester One:
GeoGebra Lab: Burning Tent Lab
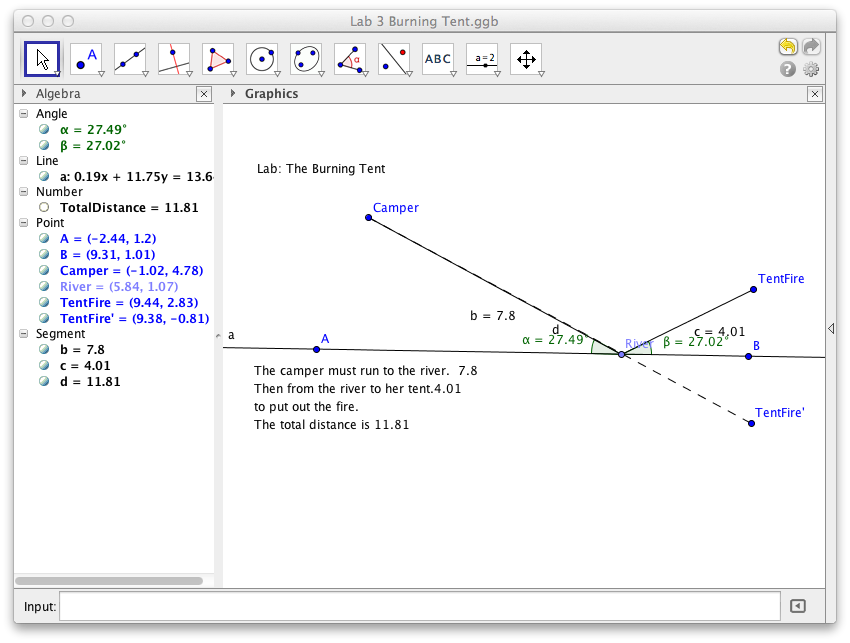
1. Once you have a minimal path, what appears to be true about the incoming angle and the outgoing angle?
The incoming angle and the outgoing angle are the same.
2. Why is the path from points Camper to TentFire’ the shortest path? Briefly explain.
The path from points Camper to TentFire’ is the shortest distance, because it is a straight line and the shortest distance between two points is a straight line.
3. Where should the point River be located in relation to segment Camper to TentFire’ and line AB so that the sum of the distances is minimized?
The point River should be on the point where the segment Camper to TentFire’ intersects with line AB.
The incoming angle and the outgoing angle are the same.
2. Why is the path from points Camper to TentFire’ the shortest path? Briefly explain.
The path from points Camper to TentFire’ is the shortest distance, because it is a straight line and the shortest distance between two points is a straight line.
3. Where should the point River be located in relation to segment Camper to TentFire’ and line AB so that the sum of the distances is minimized?
The point River should be on the point where the segment Camper to TentFire’ intersects with line AB.
Tessellations
Tessellation Project – Draft 10/10/14
Shark Bait Hoo-ha-ha
At first, the theme of my tessellation was going to be dogs, however I could not successfully create a dog shaped tile. The theme of the my tessellation is sharks. It has a fin taken from the bottom and placed on top of the shark. It has a mouth that when translated to the right side of the square is also a tail. Every row, the sharks switch direction from left to right.
My tile started with a square. I drew a tail then translated it to the other side of the square. I then sketched a fin on the bottom part of the square and placed it on the top and reflected it.
First, using a compass I made a circle on the cardboard. Then, using a ruler I added the diameter to the circle. Next, I found the perpendicular bisector of the diameter. I then connected all the points of intersection on the circle to create a square. Next, I erased the extra lines. After that construction, I cut out the square. I sketched the shark tail on the tile. I then cut out the tail. Next, I taped the tail to the opposite side of the square. Then, I drew a shark fin on the square. I cut out the fin. Finally, I flipped and taped the fin on the top of the tile.
In my opinion tessellations are both math and art. Tessellations are math, because you can use geometry to find out what polygons tessellate and which don’t. They are also art; the Merriam Webster dictionary defines art as “something that is created with imagination and skill and that is beautiful or that expresses important ideas or feelings” and tessellations can demonstrate this idea. Math skills can be used to create the translations on a tessellation; you reflect the part you cut out on to the opposite side. M.C. Esher was a graphic artist, not a mathematician, but he created detailed tessellations. “Are you really sure that a floor can’t also be a ceiling?” - M.C. Escher (see attached image). Are you really sure an art work can’t also be math?
"M. C. Escher." BrainyQuote.com. Xplore Inc, 2014. 4 November 2014. http:// www.brainyquote.com/quotes/authors/m/m_c_escher.html
Read more at http://www.brainyquote.com/citation/quotes/authors/m/ m_c_escher.html#1urglF3tBxoifcrV.99
Merriam-Webster Dictionary. N.p.: n.p., n.d. Web. 15 Oct. 2014. <http://www.merriam- webster.com/dictionary/art?show=0&t=1413404581>.
My tile started with a square. I drew a tail then translated it to the other side of the square. I then sketched a fin on the bottom part of the square and placed it on the top and reflected it.
First, using a compass I made a circle on the cardboard. Then, using a ruler I added the diameter to the circle. Next, I found the perpendicular bisector of the diameter. I then connected all the points of intersection on the circle to create a square. Next, I erased the extra lines. After that construction, I cut out the square. I sketched the shark tail on the tile. I then cut out the tail. Next, I taped the tail to the opposite side of the square. Then, I drew a shark fin on the square. I cut out the fin. Finally, I flipped and taped the fin on the top of the tile.
In my opinion tessellations are both math and art. Tessellations are math, because you can use geometry to find out what polygons tessellate and which don’t. They are also art; the Merriam Webster dictionary defines art as “something that is created with imagination and skill and that is beautiful or that expresses important ideas or feelings” and tessellations can demonstrate this idea. Math skills can be used to create the translations on a tessellation; you reflect the part you cut out on to the opposite side. M.C. Esher was a graphic artist, not a mathematician, but he created detailed tessellations. “Are you really sure that a floor can’t also be a ceiling?” - M.C. Escher (see attached image). Are you really sure an art work can’t also be math?
"M. C. Escher." BrainyQuote.com. Xplore Inc, 2014. 4 November 2014. http:// www.brainyquote.com/quotes/authors/m/m_c_escher.html
Read more at http://www.brainyquote.com/citation/quotes/authors/m/ m_c_escher.html#1urglF3tBxoifcrV.99
Merriam-Webster Dictionary. N.p.: n.p., n.d. Web. 15 Oct. 2014. <http://www.merriam- webster.com/dictionary/art?show=0&t=1413404581>.
How I Made My Tessellation Tile – 10/10/14
First, using a compass I made a circle on the cardboard.
Then, using a ruler I added the diameter to the circle.
Next, I found the perpendicular bisector of the diameter
I then connected all the points of intersection on the circle to create a square.
Next, I erased the extra lines.
After that, I cut out the square.
I sketched the shark tail on the tile.
I then cut out the tail.
Next, I taped the tail to the opposite side of the square.
Then, I drew a shark fin on the square.
I cut out the fin.
Finally, I flipped and taped the fin on the top of the tile.
Then, using a ruler I added the diameter to the circle.
Next, I found the perpendicular bisector of the diameter
I then connected all the points of intersection on the circle to create a square.
Next, I erased the extra lines.
After that, I cut out the square.
I sketched the shark tail on the tile.
I then cut out the tail.
Next, I taped the tail to the opposite side of the square.
Then, I drew a shark fin on the square.
I cut out the fin.
Finally, I flipped and taped the fin on the top of the tile.
Geogebra Lab: Snail Trail Lab
Reflection: How did you construct the “snails” and the reflective plane? What did you notice about the “snails” and their graffiti trails? What type of symmetry does your design exhibit if you ignore the color? Be specific, use the vocabulary you’ve learned: reflectional, rotational, order of rotation, angle of rotation, hexagon, line of reflection, etc.
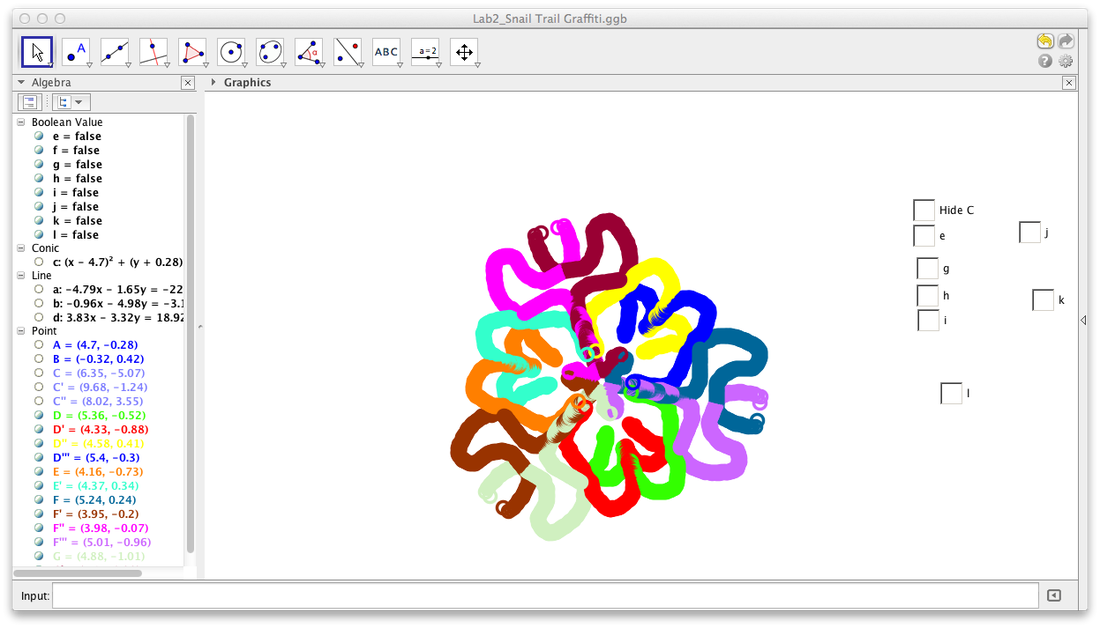
I created the “snail” by making a circle then dividing it into sixths and lacing a dot in one of the sixths. I constructed the reflective plane by reflecting the image across on of the intersecting lines. I created the I noticed that the “snails” and their trails always matched except for the colors. If I ignore the colors the construction has line/reflectional symmetry.
I created the “snail” by making a circle then dividing it into sixths and lacing a dot in one of the sixths. I constructed the reflective plane by reflecting the image across on of the intersecting lines. I created the I noticed that the “snails” and their trails always matched except for the colors. If I ignore the colors the construction has line/reflectional symmetry.
I created the “snail” by making a circle then dividing it into sixths and lacing a dot in one of the sixths. I constructed the reflective plane by reflecting the image across on of the intersecting lines. I created the I noticed that the “snails” and their trails always matched except for the colors. If I ignore the colors the construction has line/reflectional symmetry.
Snail Trail Challenge
GeoGebra Lab #2 Challenge Reflection:
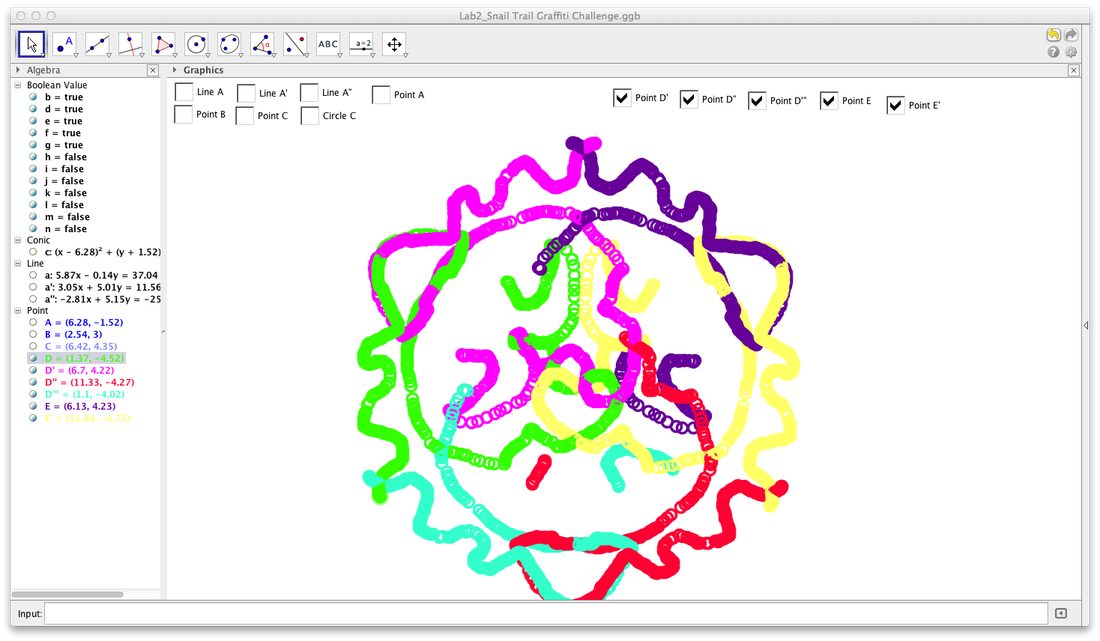
First, I constructed a circle. Then I made a line that intersected the circle in two places, Line A. Then I made a perpendicular bisector of the first intersecting line, Line A’. Next, I bisected the angle Line A and Line A’ made, and called it Line A”. I placed a dot between Line A and Line A’, and named it Point D. I then reflected Point D across Line A’ and labeled it Point D’. I repeatedly reflected points across lines until I returned to Point D. I then created check-boxes to hide/show the lines and the circle. In addition the check-boxes for the lines and circles, I created ones for all the points except for Point D.
First, I constructed a circle. Then I made a line that intersected the circle in two places, Line A. Then I made a perpendicular bisector of the first intersecting line, Line A’. Next, I bisected the angle Line A and Line A’ made, and called it Line A”. I placed a dot between Line A and Line A’, and named it Point D. I then reflected Point D across Line A’ and labeled it Point D’. I repeatedly reflected points across lines until I returned to Point D. I then created check-boxes to hide/show the lines and the circle. In addition the check-boxes for the lines and circles, I created ones for all the points except for Point D.